信息安全数学基础3
3同余式
3.1一次同余式
同余式是数论的基本概念之一,设m是给定的一个正整数,a、b是整数,若满足$m|(a-b)$,则称a与b对模m同余,记为$a≡b(mod m)$,或记为$a≡b(m)$。这个式子称为模m的同余式,若m∤ (a-b),则称a、b对模m不同余,同余概念又常表达为:$a=b+km(k∈Z)$;
3.1.1一次同余式的求解
需注意的是:同余式的解不是,按我们以往那样认为的是一个或某个解,它是一类解,即某个剩余类。
思想:利用同余和整除的相互转化
定理:若$(a,m)=1,(m \ge 1)$,则$ax \equiv b \pmod{m}$恰有一解。
证明:
$$ax \equiv b \pmod m \Rightarrow ax=b-my$$
$ax+my=b$ 有解要求$(a,m)|b$,但如果$(a,m)=1$,则对$b$不做要求。在$0 \le x\le m-1$范围内,$x$有唯一解
求解方式一:
用M的完全剩余系一一带入求解,观察是否符合条件。
唯一解$x$的表达式推导:
$\because (a,m)=1$
$\therefore a^{\varphi(m)} \equiv 1 \pmod m $ (欧拉定理)
$\therefore a(a^{\varphi (m)-1} b) \equiv b \pmod m$
$\therefore x\equiv a^{\varphi (m)-1} b$
圈起来,要考!!!!
拓展定理:若$(a,m)=d$,$d|b$。则$ax \equiv b \pmod m$有$d$个解,
$\because (a,m)=d$
$\therefore (\frac{a}{d},\frac{m}{d})=1$
$\therefore (\frac{a}{d})x \equiv1 (\bmod \frac{m}{d})$
恰有一解$x_0$
这里可以直接用上文的公式:$\therefore x\equiv a^{\varphi (m)-1} b$
$x_1 \equiv \frac{b}{d} \cdot x_0 \pmod{ \frac{m}{d}}$是其中一个解
其通解为:$x \equiv x_1 + t \cdot \frac{m}{d} \pmod{m}$,其中$t=0,1,2,3….(a,m)-1$
要求通解,就需要先求出$x_0,x_1$
3.1.2一次同余式在仿射加密中的应用
在普通的移位密码中,如凯撒密码,在加密后,字母的先后顺序没有变(因为它是全体偏移某一个数),且密钥量太小(你最多就把a换成z,再往后就循环了)
一次同余式可以在仿射加密中做出一定程度改进,但核心还是没有变化。
《信息安全数学基础》31页 eg 3.5
3.2中国剩余定理(韩信点兵)
原理:利用同余的性质,在计算中可以把$mod ;M$换成$mod ; m$。$M$代表大数字,$m$代表小数字
感谢:https://www.youtube.com/watch?v=bFisuyRQEGk
今有物不知何数,三三数之剩二,五五数之剩三,七七数之剩二。问物有几何?
再讲一下这题的思路,以此说明中国剩余定理干吗的?
在这题,我们模一个很大的数,有些困难,那我们就把它变成模两个小的数字
$x \equiv s \pmod{xyz}$
$x\equiv x_1\pmod{x}$
$x\equiv x_2\pmod{y}$
$x\equiv x_2\pmod{z}$
$x=a+b+c$
回到题目:
$x\equiv2\pmod{3}$
$x\equiv3\pmod{5}$
$x\equiv2\pmod{7}$
$x = a + b +c$,分别求出$a,b,c$
解:
$x\equiv2\pmod{3}$
$x\equiv 0\pmod{5}$
$x\equiv 0\pmod{7}$
$a$所需满足条件$a=5 \times 7\times p$(a为35的倍数),同时$a\equiv2\pmod{3}$
$a=35$
$x\equiv 0\pmod{3}$
$x\equiv 2\pmod{5}$
$x\equiv 0 \pmod{7}$
$b$所需满足条件$b=3 \times 7\times p$(b为21的倍数),同时$b\equiv 3\pmod{5}$
$$b=63$$
同理得$c=30$
$x=a+b+c=35+63+30=128$是其中一组解
相当于$m=3 \times 5 \times 7 =105$
$x \equiv 128 \pmod{105}$
$X$解的范围是 $x + 3\times5\times7 \timest=128+105t$
可以根据情况取相应解。此物的数量为23
eg:

 这里大数变小数,相当于绕了一下。
这里大数变小数,相当于绕了一下。
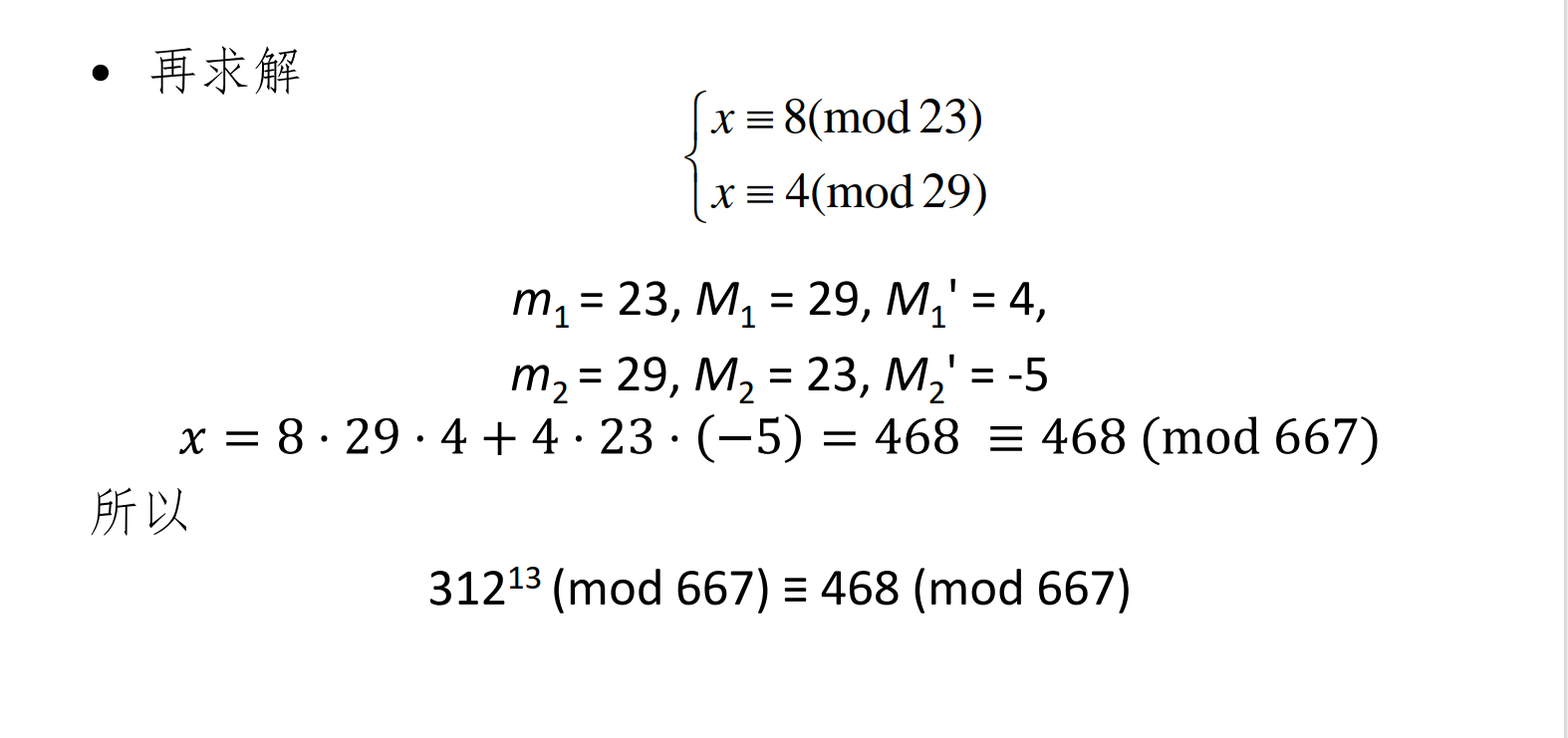
然后继续使用中国剩余定理,求解。
再讲一下这题的思路,以此说明中国剩余定理干吗的?
在这题,我们模一个很大的数,有些困难,那我们就把它变成模两个小的数字
l
3.3同余式的应用·
3.3.1RSA公钥密码系统
感谢:https://www.youtube.com/watch?v=TqX0AHHwRYQ
背景:对极大整数做因数分解的难度决定了RSA算法的可靠性
加密过程: $m^e \bmod n = c$
解密过程: $c^d \bmod n = m$
$n=q \times p$即两个大素数相乘
取得$n$的欧拉数$\varphi(n) = (p-1) \times (q-1)$
$e$的选取范围$1 <e< \varphi(n)$,要求是$e$与$\varphi(n)$互素,当然最好$e$不要太小,不然可能被爆出来。
核心原理:它利用$$d \cdot e \equiv 1 \pmod{\varphi(n)}$$
即$$m \cdot d \cdot e \equiv m \pmod{\varphi(n)}$$
$e$和$n$是公钥
$d$为私钥
《信息安全数学基础》36页
3.3.2CTR在RSA中的应用
这就是前文讲中国剩余定理的原因。
作用:使解密速度加快
《信息安全数学基础》37页
e的选取不可太小,若加密指数为e,当获得明文的e个密文,即可获得明文
3.3.3模重复平方算法
作用:无论是加密还是解密中,都会就算模幂,此方法可提高效率